Matemātika mums ir palīdzējusi atrisināt dažus no pasaules lielākajiem noslēpumiem. Mēs apskatīsim dažus piemērus un iepazīstināsim jūs ar 5 mīklām, lai pārbaudītu jūsu matemātikas prasmes un jums palīdzētu aptvert, cik aizraujoši iespējams mācīties matemātiku!

Kāda nozīme ikdienas dzīvē ir atjautības uzdevumiem matemātikā

Matemātika jau kopš seniem laikiem ir bijusi neatņemama mūsu ikdienas dzīves sastāvdaļa. Mūsu nemitīgā vēlme paplašināt zināšanas ir aizvedusi mūs tik tālu, ka šodien pasaule, kādu mēs to pazīstam, nebūtu iespējama bez matemātikas. Matemātika ir ieviesusi kārtību dažādās sabiedrībās uz šīs planētas, kā arī novērsusi haosu un katastrofas. Daudzas no mūsu cilvēciskajām īpašībām, piemēram, telpisko apziņu, problēmu risināšanas prasmes, spēju spriest un pat radošumu un komunikāciju, attīsta un pilnveido matemātikas teorijas.
Lietas, kas, šķiet, nav saistītas ar matemātiku, patiesībā ir saistītas ar vajadzību pēc matemātikas un tās struktūras, ko tā ienes mūsu ikdienas dzīvē.
neatkarīgi no tā, vai esat mākslinieks vai zinātnieks.
Gleznotājs izmantos savu radošumu apvienojumā ar izpratni par visām lietām, kas atrodas tieši viņa priekšā, kā arī par lietām ap viņu. Viņi (apzināti vai neapzināti) ar katru otas triepienu plāno un aprēķina, cik gara un iedarbīga būs zīme, ko viņi liek uz audekla, kā tā būs saistīta ar pārējo darbu un kā tā sasaucas ar plašāku mākslinieka vidi. Turklāt māksliniekiem būs nepieciešams budžets tādām lietām kā piederumi, instrumenti, studiju īre u. c. Viņiem vajadzēs izmantot loģisko domāšanu un skaitļus, lai noteiktu atbilstošas cenas saviem mākslas darbiem.
Pavisam noteikti, - zinātnieks ikdienā tieši saskarsies ar skaitļiem, mērījumiem, vienādojumiem un formulām, un matemātika valdīs visos pētījumos, ko viņš veic. Jā, tas viss izklausās pārāk nopietni un diezgan biedējoši, vai ne? Teikt, ka matemātika regulē gandrīz visu šajā pasaulē un ka tās nozīme dzīvē ir neaptverama? Sabiedējām? Neuztraucieties, tagad sāksies interesantākā daļa!
Matemātikas problēmu pārvēršana ieguvumos - atjautības uzdevumi un galvas mežģi
Daudziem, parasti tiem, kas saskaras ar grūtībām, apgūstot matemātiku, tā šķiet garlaicīgs mācību priekšmets. Bet tā patiešām nav!
Ieviešot matemātikas teoriju un jēdzienu apguvē izklaidējošus elementus, daudz vairāk skolēnu gūtu panākumus šajā jomā!
Ir ļoti vienkārši atslēgties un neuzņemt nekādu informāciju, ja mums nav intereses. Savukārt veids, kā saglabāt un apstrādāt svarīgu informāciju un neļaut tai vienkārši “ieiet pa vienu ausi iekšā, pa otru ārā”, - ir ar prieku pieslēgties konkrētajai tēmai.
Vai zinājāt, ka, apgūstot matemātiku un tās daudzos trikus un mīklas, jūs varat aizraujoši pavadīt laiku? Vairums no mums nevar noliegt, ka labi atjautības uzdevumi un sarežģītu loģikas mīklu risināšana ir fantastisks smadzeņu mežģis. Padarīt mācības ar algebru, daļskaitļiem un varbūtības teoriju aizraujošas nav nemaz tik grūti, kā iesākumā varētu šķist! Ja neticat, tad izmēģiniet šīs matemātikas mīklas!
Jā, patiešām ir iespējams vingrināties matemātikā, vienlaikus šo procesu izbaudot! Neatkarīgi no tā, vai tā ir optiskā ilūzija, attēlu puzle vai loģiskās spēles, sarežģītas mīklas atbildes uzminēšana ir lielisks veids, kā uzlabot problēmu risināšanas prasmes.
Pārbaudiet savu matemātikas loģiku ar sarežģītiem atjautības uzdevumiem
Lai izprastu apkārtējo pasauli, cilvēks ir izmantojis matemātiku, cenšoties iegūt taustāmus pierādījumus. Matemātikas vēsturi caurvij lieli prāti, kas cīnījās ar sava laika lielajām mīklām.
Matemātiskās mīklas un atjautības uzdevumi apvieno domāšanu ar skaitļiem, aprēķiniem un figūrām. Lai atrisinātu šādas mīklas, nav nepieciešams būt matemātikas ģēnijam, bet ir svarīgi izmantot loģisku pieeju un pielietot matemātikas prasmes, kas apgūtas mācību programmā, - sākot ar vienkāršu reizināšanu un dalīšanu, kvadrātvienādojumiem un rēķināšanu. Tāpēc gatavojieties izvingrināt savu iekšējo matemātiķi, risinot šos 5 sarežģītos uzdevumus, ar kuriem var nākties saskarties matemātikas stundās. Bet vispirms padomāsim, kā un kāpēc šie prāta mežģi mums ir tik noderīgi.
Priekšrocības, ko sniedz matemātikas galvas mežģi
Tas viss nav tikai un vienīgi jūsu galvā! Tas ir smadzeņu treniņš visam jūsu ķermenim un labsajūtai.
Tikai aizdomājieties: ja, piemēram, viens vienīgs slavenības attēls, kas izskatās perfekti, var izraisīt spēcīgu motivāciju doties uz sporta zāli, pirkt jaunas drēbes, mainīt matu sakārtojumu utt., tad arī viena maza matemātiska spēle var mainīt jūsu domāšanu un likt kaut kam galvā noklikšķēt! Kas zina, ko regulāra smadzeņu trenēšana varētu darīt attiecībā uz to, kā jūs skatāties uz matemātiku un kā domājat par lietām kopumā!
Tālāk ir formula, kas jums varētu patikt un kas varētu attiekties uz jums, ja mācāties matemātiku.
kontrole = pilnveidošanās = apmierinātība
Galvas mežģi
100 ieslodzīto problēma
Kādā cietumā atrodas 100 uz nāvi notiesāti ieslodzītie. Cietuma direktors izsaka izaicinājumu un katram ieslodzītajam piešķir numuru no 1 līdz 100. Pēc tam viņš savā kabinetā iekārto skapi ar 100 atvilktnēm. Katrā no tām ir skaitlis no 1 līdz 100, kas atbilst ieslodzītajiem piešķirtajiem numuriem. Katrs skaitlis lietots tikai vienu reizi.
Direktors lūdz, lai katrs ieslodzītais atver 50 atvilktnes un pārbauda, kāds skaitlis tajās atrodas. Direktora kabinetā ieslodzītajiem ir aizliegts ar citiem sazināties, kā arī mainīt atvilktņu secību vai atstāt kādas norādes. Neviens ieslodzītais nezinās, kādus numurus redzējuši citi.

Cietuma direktors norāda divus iespējamos iznākumus:
- Visi ieslodzītie atrod savus attiecīgos numurus un visi tiek apžēloti.
- Neviens no ieslodzītajiem neatrod savu numuru, un viņiem visiem tiek izpildīts nāvessods.
Kāda ir iespēja, ka katrs ieslodzītais atradīs atvilktni, kas atbilst viņa numuram? Saskaņā ar matemātiskās varbūtības likumu iespēja, ka visi tiks apžēloti, ir (1/2)100 jeb 0,0000000000000000000000000000008.
💡Pastāv gudra stratēģija, kas piedāvā ieslodzītajiem iespēju palielināt šīs izredzes un palikt dzīviem. Kāda tā ir?
Trīs dievi
Aiz trim simboliem A, B un C slēpjas 3 dievi, kas pazīstami kā “patiess”, “nepatiess” un “nejaušs”. "Patiesais” dievs vienmēr atbild patiesību, “nepatiesais” vienmēr melo, bet “nejaušais” neparedzami mainās starp abiem dieviem.
💡Izaicinājums ir “vienkāršs”! Atklājiet A, B un C identitātes, uzdodot tikai trīs jautājumus, uz kuriem atbilde ir vai nu patiesa, vai nepatiesa. Katru jautājumu var uzdot tikai vienam dievam, bet, ja nolemjat uzdot jautājumu vienam dievam vairāk nekā vienu reizi (ne vairāk kā trīs reizes), pārējie dievi nevarēs atbildēt. Jūsu jautājumi var būt savstarpēji nesaistīti.
Trīsstūrveida kūka
Gatavojot klasi matemātikas konkursam, skolotājs nolemj piedāvāt skolēniem tortes trīsstūra formā ar trim nevienādām malām. Viņš veic pasūtījumu kūku veikalā, norādot kūkas trīs malu izmērus. Konditors pasūta kūkas kasti, norādot tos pašus izmērus. Tomēr, kad kūka ir gatava, viņš konstatē, ka, lai gan mērījumi ir ievēroti, kastes forma ir simetriska, nevis identiska tās kūkai. Viņš zvana matemātikas skolotājam, lai pajautātu, kā sagriezt kūku, lai tā ietilptu kastē. Skolotājs atbild, ka pietiks ar diviem griezumiem.
💡Kādiem šiem griezumiem jābūt?
Kaķa un peles problēma
Kaķis un pele nolemj spēlēt "ar galvu vai asti", bet viņi nolemj mainīt noteikumus: katram spēlētājam jāizvēlas 3 kombinācijas (piemēram, galvas, astes, galvas). Viņi met monētu vairākas reizes, un spēlē uzvar tas, kurš pirmais trīs reizes pēc kārtas metot monētu redz vienu no kombinācijām. Abi spēlētāji nevar izvēlēties vienu un to pašu kombināciju. Kaķis, uzskatot sevi par spēcīgāku spēlētāju, sāk pirmais. Pele, kas ir gudrākā no abiem, nolemj ļaut viņam sākt.
💡Kā var palielināt katra spēlētāja izredzes uz uzvaru?
Pīle un kaķis
Apļveida dīķa vidū ir pīle. Dīķa malā atrodas nepacietīgs kaķis. Kamēr pīle labprāt nogaršotu zāli dīķa malā, kaķis ļoti labprāt nogaršotu pīli! Kaķis neprot peldēt un pārlieku baidās no ūdens, lai ietu dīķī. Savukārt pīlei ir pārāk mazi spārni, lai tā varētu lidot.
💡Zinot, ka kaķis var skriet četras reizes ātrāk nekā pīle peldēt, vai pīlei ir iespēja sasniegt dīķa malu tā, lai kaķis viņu nenoķertu?
Vēl daži matemātikas galvas mežģi, lai pārbaudītu jūsu matemātikas spējas
Galvas mežģis ir jautājums, uz kuru būtu jāatbild atjautīgi. Tiesa, ne visiem patīk galvas mežģi. Un šādā gadījumā tie drīzāk sagādā neapmierinātību, nevis jautri pavadītu laiku. Taču, tiklīdz tos izpratīsiet, arī jums tie liksies amizanti.
Ir dažāda veida galvas mežģi. Daži no tiem ir balstīti uz apstākļiem vai situācijām, citi - uz noteiktu secību.
Piemēram:
💡Marijas tēvam ir piecas meitas: Nana, Nene, Nini un Nono. Kāds ir piektās meitas vārds?
Daži varētu sekot līdzi patskaņu sistēmai un nosaukt piekto meitu par Nunu, taču, kā jau tas bieži gadās prāta mežģu gadījumos, atbilde ir meklējama jautājumā. Ja Marijas tēvam ir piecas meitas, tad Marijai jābūt vienai no tām... vai ne?
Matemātikas prāta mežģiem var būt arī šādas acīmredzamas atbildes, bet dažreiz ir nepieciešams vairāk padomāt. Piemēram:
💡Ja trīs putni trīs dienās izdēj trīs olas, cik olu viens putns izdēj vienā dienā?
Atbilde uz šo jautājumu ir neviennozīmīga. No matemātiskā viedokļa raugoties, viens putns vienā dienā izdēj 1/3 olu. Tomēr, tā kā neviens cilvēkam zināms putns nevar dēt tikai vienu trešdaļu olas, loģiska atbilde ir vai nu vienu, vai nevienu.
Vai tagad saprotat, ko mēs domājām, sakot, ka ne visiem patīk prāta mežģi?
Prāta mežģiem jābūt atbilstošiem līmenim. Respektīvi, ir tikai dabiski, ka mēs nevēlamies mocīt matemātikas skolēnus ar mīklām, kas prasa zināšanas par augstākām algebriskām sistēmām, kad viņi vēl nav nonākuši šajā mācību posmā!
Galvas mežģi jaunākiem skolēniem
💡Nepieciešams nedaudz saskaitīšanas: kā, izmantojot tikai 8 astotniekus, tos saskaitīt kopā, lai tie būtu vienādi ar 1000?
Atbilde: 888+88+88+8+8+8+8 = 1000
💡Es domāju par trīsciparu skaitli. Otrais cipars ir četras reizes lielāks par trešo, bet pirmais ir par trim mazāks par otro.
Atbilde: 141
💡Kurus trīs skaitļus saskaitot vai reizinot kopā, iegūst vienu un to pašu rezultātu?
Atbilde: 1, 2 un 3
💡Pirmdien Andris uztaisīja četras sniega bumbas. Otrdien viņš izveidoja deviņas, bet trešdien - 14. Cik viņš uztaisīja ceturtdien un piektdien?
Atbilde: katru dienu palieliniet summu par pieciem.
Padziļinātāki galvas mežģi jeb cietie rieksti
💡Janvārī augstākā Rīgā reģistrētā temperatūra bija -1 grāds. 2. janvārī bija 4 grādi. Kāda bija temperatūra 3. janvārī, ja janvāra pirmo trīs dienu vidējā temperatūra bija 2 grādi?
Atbilde: 3 grādi
💡Kāds hotdogu tirgotājs vēlas nopirkt vienādu daudzumu desiņu un bulciņu. Vienā iepakojumā bulciņas ir 10, bet desiņas - 8. Cik iepakojumu no katra produkta tirgotājam būtu jāpērk, lai sasniegtu savu mērķi?
Atbilde: 10 iepakojumi desiņu un 8 iepakojumi bulciņu.
💡Visi šie apgalvojumi ir patiesi: AxB=12; A+B+C=12; un B-A=1. Kādus skaitļus apzīmē A, B un C?
Atbilde: A=3, B=4, C=5
Atšķirība starp galvas mežģiem un atjautības uzdevumiem
Daudzi cilvēki nenošķir šo divu veidu prāta līkločus. Galu galā tie abi ir jautājumi, kas paredzēti, lai liktu jums domāt... vai ne? Atšķirība starp galvas mežģiem un atjautības uzdevumiem ir to nolūks.
Dažkārt atjautības uzdevumos tiek izmantotas divdomības vai izmantotas atšķirīgas frāzes, kuru atrisināšanai nepieciešama atjautība un netradicionāla domāšana. Šeit ir lielisks piemērs:
💡Kas sākas ar A, beidzas ar A un kurā ir A? Anagramma.
Galvas mežģi parasti ir domāti izklaidei, tāpēc tie būtu efektīvi kā iesildīšanās vai ledlauzis matemātikas stundas sākumā.
uzlabo noskaņojumu un garīgi sagatavo skolēnus mācībām.
Aprūpētāji! Arī jūs varat attīstīt savu aprūpējamo domāšanu, laiku pa laikam piedāvājot galvas mežģus.
Esat sastrēgumā? Gaidāt pie ārsta? Lielisks laiks prāta vingrināšanai!

Loģiskās puzles matemātikā
Tāpat kā tradicionālās puzles, kuru savstarpēji savienotie elementi veido pilnīgu attēlu, arī loģiskās puzles darbojas pēc tāda paša principa tikai bez elementiem. Loģiskās puzles liek uzdevuma dalībniekam pareizi salikt šos tēlainos gabaliņus kopā, izmantojot tikai savu domāšanu... un, iespējams, zīmuli, lai veiktu piezīmes. Dažas no populārākajām loģiskajām puzlēm, kurās iesaistīti skaitļi, ir Sudoku un KenKen. Viena īpaša loģikas puzle, kas pāršalca pasauli un pat bija Holivudas kinolentes “The Pursuit of Happiness” galvenā tēma, ir… Vai spējat atrast pareizo atbildi?
Rubika kubs, arhitekta Erno Rubika ideja, apbūra pasauli uzreiz pēc tā pirmizrādes 1980. gadā. Kopš tā laika no sākotnējā kubika koncepta ir izveidotas vairākas iterācijas: Rubika čūska un Rubika maģija, kā arī daudzas pēc pasūtījuma veidotas puzles un pat digitālās versijas.

Mūsdienās, vairāk kā 40 gadus pēc šī kuba debijas, visā pasaulē notiek ātrās kubošanas sacensības. Dažas no tām ir paredzētas akliem cilvēkiem, citas – šī kuba likšanai ar kājām. Un, protams, kubu puzles atrisināšanai pēc iespējas īsākā laikā. Pasaules Kuba Asociācija regulē un sponsorē šos pasākumus.
Rubika kungs izdomāja kubu kā izaicinājumu saviem studentiem - tolaik viņš bija arhitektūras profesors. Ierīce, kas bija izgatavota no koka un savienota ar gumijas lentēm, bija paredzēta, lai skolēniem sniegtu praktisku pieredzi, manipulējot ar trīsdimensiju objektu. Viņš nebija iecerējis izveidot loģisko puzli un pat neapzinājās, ka tā ir loģiskā puzle, līdz mēģināja atjaunot tās sākotnējo stāvokli - visas krāsas bija savās pusēs.
Vai varat izdomāt jaunu algoritmu, kā to atrisināt?
Šeit ir dažas citas loģiskās puzles, kurās varat izmēģināt spēkus. Diemžēl ar tām nevar darboties fiziski kā ar Rubika kubu!
💡Jums ir maisiņš ar 10 āboliem. Jūs sastopat 10 draugus, no kuriem katrs vēlas vienu ābolu. Jūs sadalāt ābolus - pa vienam katram draugam, un maisiņā paliek viens. Kā tas ir iespējams?
Atbilde: jūs atdevāt pēdējam draugam maisiņu ar pēdējo ābolu.
💡Jums ir trīs mazi maisiņi, katrā ir divas bumbiņas. Maisiņā Nr. 1 ir divas zilas bumbiņas, maisiņā Nr. 2 ir divas zaļas bumbiņas, bet maisiņā Nr. 3 ir viena zaļa un viena zila bumbiņa. Ieliekot roku vienā maisiņā, jūs izņemat zilu bumbiņu; cik ticams, ka šajā maisiņā palikusī bumbiņa ir zila?
Atbilde: ir 2/3 varbūtība, ka arī atlikusī bumbiņa būs zila.
💡Kā var saskaitīt divus trīsciparu skaitļus, lai vienmēr būtu vienāds ar 1089?
Atbilde: izvēlieties trīsciparu skaitli un pēc tam to apgrieziet. Atņemiet sākotnējo skaitli no apgrieztā skaitļa un šo rezultātu apgrieztiet. Pievienojiet šo skaitli atņemšanas rezultātam, lai iegūtu 1089.
💡4 collu masīva koka kubs ir nokrāsots sarkanā krāsā no visām 6 šķautnēm. Pēc tam to sagriež 1 collas kubiņos. Cik daudziem no šiem kubiem būs 3 sarkanas malas, cik daudziem būs 2 sarkanas malas vai 1 sarkana mala un cik kubiem nebūs sarkanas krāsas?
Atbilde: 8 kubiem būs 3 sarkanas malas, 24 kubiem būs 2 sarkanas malas, 24 kubiem būs 1 sarkana mala un 8 kubiem nebūs sarkanas krāsas.
Dažas no šīm puzlēm šķiet pretrunā ar loģiku, piemēram, 2. jautājumā:
- Kā var būt 2/3 varbūtība, ka otra bumbiņa būs zila, ja zaļo bumbiņu skaits ir lielāks par zilo? Šī parādība ir pazīstama kā Monte Hala problēma, un tās pamatā ir intuīcija un izslēgšana.
- Jūs varat izslēgt maisiņu, kurā ir tikai zaļas bumbiņas; acīmredzot jūs no tā neesat izvēlējies. Atliek 2 maisiņi. Katrā no tiem ir pa zilai bumbiņai.
- Tagad, kad esat (tēlaini) likvidējis 2 zaļās bumbiņas, zilo bumbiņu skaits, kas joprojām ir maisiņos, ir divreiz lielāks par zaļo bumbiņu skaitu…
- Tā kā kopējais bumbiņu skaits, no kurām var izvēlēties, ir 3 un divas no tām ir zilas, jums ir 2 pret 3 iespēja atkal izvēlēties zilu.
Lielākā daļa uzskata, ka jums būs 50 % iespēja atkal izvēlēties zilo krāsu, bet tagad, kad esam veikuši matemātiskos aprēķinus, redzam, ka šis pieņēmums nav pareizs!
Līdzīgi ir ar sarkani krāsoto kubu. Šķiet, ka daudzi pieņem, ka kubs ir tukšs, un aizmirst pievienot astoņus neapkrāsotos kubus, kas veido lielākā kuba kodolu.
Visbeidzot, ābolu maiss un visi šie alkatīgie draugi: daudzi nojauš, ka katrs ābols tiks izņemts no maisa, lai to atdotu, bet tas ir nepieciešams tikai pirmajiem deviņiem āboliem. Ļaujiet desmitajam alkatīgajam draugam atbrīvoties no ābolu maisa jūsu vietā!
Kas attiecas uz trīs cipariem, kuru kopsumma vienmēr ir 1089... Patiesībā ir diezgan interesanti redzēt, cik jautri var būt spēlēties ar algebru!
Bonuss! Trīs atjautības uzdevumi matemātikā
Ja jums patīk jautras matemātikas spēles, vārdu uzdevumi vai atjautības uzdevumi, jums patiks arī šīs puzles:
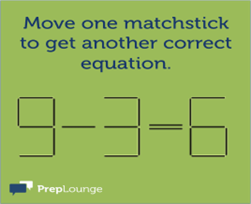
💡Pārvietojiet vienu sērkociņu, lai iegūtu citu pareizu vienādojumu.
Atbilde: ir divas iespējas: 3 + 3 = 6 un 8 - 3 = 5

💡Kāda ir vērtība 1/2 no 2/3 no 3/4 no 4/5 no 5/6 no 6/7 no 7/8 no 8/9 no 9/10 no 1000?
Atbilde: 100

💡Palīgs: otrajam ciparam nav nozīmes rezultāta iegūšanai.
Atbilde: pirmais cipars reiz pirmais cipars, trešais cipars reiz trešais cipars.
398 = 964 (3x3 8x8)
118 = 164 (1x1 8x8)
356 = 936 (3x3 6x6)
423 = 169 (4x4 3x3)
Matemātikas atjautības uzdevumi un nodarbības
Mīlēt matemātiku... vai nemīlēt?
Vai mums visiem vajadzētu mīlēt matemātiku un matemātiskos vienādojumus? Kāpēc tie ir svarīgi? Kāpēc daži cilvēki norobežojas, kad runa ir par šo tēmu?
Kādi ir iemesli, lai mums patiktu risināt atjautības uzdevumus matemātikā?
- Ar matemātikas palīdzību var noskaidrot, vai kaut kas ir patiess vai nepatiess.
- Matemātiskajās teorijās ir zināma elegance. Tā kā tās ir ļoti kodolīgas un vienkāršas, jūs, iespējams, konstatēsiet, ka varat iegūt jaunu izpratni tikai ar nelielu mācību apjomu. Svarīgākais ir vienmēr censties saprast, nevis apgūt desmitiem formulu un teorēmu, neizprotot to būtību.
- Matemātika pokerā var būt ļoti noderīga, kad runa ir par pareizu likmju likšanu!
- Matemātika ir ļoti spēcīgs instruments: ar to ir iespējams sasniegt izcilus rezultātus un pielietojumus, kas sākotnēji šķiet nesasniedzami.
- Pateicoties matemātikai, jūs ne tikai padziļināti izpratīsiet apkārtējo pasauli, bet arī labāk spēsiet apgūt citas nozares, piemēram, fiziku, ķīmiju un ekonomiku.
- Matemātika ir kā spēle, jo tā darbojas loģiski, formāli un stimulē smadzenes. Piemēram, kā šahs, sudoku un pat Candy Crush Saga!
- Kad esat apguvis galvenos principus, matemātika kļūst par jūsu otro dabu, kas palīdz jums saprast un risināt apkārtējās problēmas.
Matemātikai ir sava valoda, un, lai to labi lietotu, ir jāapgūst tās specifiskā gramatika, vārdu krājums un pareizrakstība. Ir noteikumi, kas ir obligāti jāapgūst, un tie ir bez šaubām jāpielieto.
Matemātika ir izaicinājumu pilna mācību disciplīna, kas prasa regulāru praksi un lielu pašdisciplīnu. Ar "gandrīz" matemātikā nepietiek: ir jābūt precīzam un metodiskam. Neatkarīgi no tā, vai esat viens pats pie ekrāna vai mācību grāmatas, vai apmeklējat nodarbības pie privāta matemātikas pasniedzēja, jums ir jābūt centīgam un neatlaidīgam, jo īpaši ārpus tradicionālajām matemātikas nodarbībām, ja jūs apgūstat šādu mācību programmu.
Ko jūs varat apgūt matemātikas kursos?
Vispārējais vidējās izglītības sertifikāts
Saskaņā ar valdības noteiktajām prasībām matemātikā skolēniem ir jāvar:
- Pilnveidot zināšanas, prasmes un izpratni par matemātiskām metodēm un jēdzieniem.
- Apgūt, izvēlēties un pielietot matemātiskās metodes problēmu risināšanai.
- Matemātiski spriest, izdarīt secinājumus.
- Saprast, interpretēt un sniegt matemātisko informāciju dažādos veidos, kas atbilst informācijai un kontekstam.
Šī kursa laikā galvenās tēmas, ar kurām jūs saskarsieties matemātikā, ir:
- skaitļi,
- algebra.
- attiecības, proporcijas un izmaiņu koeficienti,
- ģeometrija un mērvienības,
- iespējamība,
- statistika.
Vai šeit ir vieta arī kādai izklaidei? Tomēr nav nekas slikts, ja pajautāsiet, vai jūsu skolotājs ir dzirdējis par šīm foršajām matemātikas spēlēm un vai jūs varētu izmēģināt dažas līdzīgas mīklas un spēles klases stundā!
A līmenis
Valdība uzskata, ka A un AS līmeņa skolēniem ir svarīgi:
- Izprast matemātiku un matemātiskos procesus tādā veidā, kas veicina pārliecību, sekmē baudu un nodrošina stingru pamatu turpmākai mācību gaitai.
- Paplašināt matemātisko prasmju un metožu klāstu.
- Izprast matemātikas konsekvenci un progresu un to, kā dažādas matemātikas nozares ir savstarpēji saistītas.
- Pielietot matemātiku citās studiju jomās un apzināties matemātikas nozīmi darba vidē un citās sabiedriskās situācijās kopumā.
- Izmantot savas matemātiskās zināšanas, lai pieņemtu loģiskus un pamatotus lēmumus, risinot problēmas gan tīrā matemātikā, gan dažādos kontekstos, un skaidri izskaidrot šo lēmumu matemātisko pamatojumu.
- Loģiski spriest un atpazīt nekorektu argumentāciju.
- Konstruēt matemātiskus pierādījumus.
- Izmantot matemātiskās prasmes un metodes, lai risinātu sarežģītas problēmas, kuru risināšanai ir jāizvēlas risinājuma stratēģija.
- Atpazīt, kad matemātiku var izmantot, lai analizētu un atrisinātu problēmu kontekstā.
- Matemātiski attēlot situācijas un izprast saikni starp problēmām un matemātiskajiem modeļiem, ko var izmantot to risināšanai.
- Zīmēt diagrammas un zīmēt grafikus, lai palīdzētu izpētīt matemātiskas situācijas un interpretēt risinājumus.
- Izdarīt secinājumus, slēdzienus un izteikt pieņēmumus, izmantojot matemātisko argumentāciju.
- Interpretēt risinājumus un efektīvi informēt par to interpretāciju problēmas kontekstā.
- Lasīt un saprast matemātiskus argumentus, tostarp metožu un formulu pamatojumus, un paziņot savu izpratni.
- Lasīt un saprast rakstus par matemātikas lietojumiem un informēt par savu izpratni.
- Efektīvi izmantot tehnoloģijas, piemēram, kalkulatorus un datorus, un atpazīt, kad to izmantošana var būt nepiemērota.
- Uzņemties arvien lielāku atbildību par savu mācīšanos un savas matemātikas attīstības novērtēšanu.
Tāpēc A līmeņa matemātikas kursa galvenās tēmas ir šādas, un katru sadaļu veido daudzas apakštēmas:
- matemātiskie argumenti, valoda un pierādījumi,
- matemātisko problēmu risināšana,
- matemātiskā modelēšana.
Bakalaura grāds matemātikā
Studiju laikā jūs varat izvēlēties specializāciju, piemēram, matemātiskās finanses, matemātisko fiziku, matemātisko bioloģiju, aktuāro matemātiku, matemātikas vēsturi, speciālo relativitātes teoriju, kvantu teoriju vai medicīnas statistiku, lai gan daudzas no šīm jomām ir pieejamas kā atsevišķi kursi matemātikas bakalaura grāda vēlākajos gados.
Tēmas, kuras jūs apgūsiet matemātikas studiju programmas ievadgada laikā, ir šādas:
- algebra,
- analīze,
- mehānika,
- varbūtība,
- statistika,
- ģeometrija,
- vektori,
- skaitļošanas matemātika.
Protams, pat ja jums patīk matemātika un domājat, ka esat pietiekami labs matemātikā (💡un pēc visām šīm atjautības spēlēm jūs noteikti tāds būsiet!), tad jums nav jāmācās tikai matemātika. Kāpēc kā lieliskas idejas neizskatīt ekonomiku, inženierzinātnes, datorzinātnes, fiziku vai teorētisko fiziku, vai kādu citu zinātņu priekšmetu, piemēram, ķīmiju, bioloģiju vai psiholoģiju, grāmatvedību vai finanses?
Kur matemātika var jūs aizvest profesionālajā jomā?
Ja vēlaties strādāt finanšu jomā, ir nepieciešama zināma līmeņa matemātikas kvalifikācija, taču jums nav obligāti nepieciešams grāds. Iespējams, jums būtu vērts apsvērt šādas jomas: grāmatvedība, investīciju pārvaldība, investīciju banku pakalpojumi un banku pakalpojumi privātpersonām.

Papildus finanšu nozarei ir arī tādas nozares kā inženierzinātnes un informācijas tehnoloģijas, kurās var noderēt cilvēks, kas labi pārzina skaitļus. Matemātikas studiju absolventi var ieņemt arī tādus amatus kā aizsardzības un izlūkošanas virsnieks, statistiķis, operatīvais pētnieks, akadēmiskais matemātiķis, matemātikas skolotājs pamatskolā vai vidusskolā, kā arī strādāt jurisprudences, plašsaziņas līdzekļu, uzņēmējdarbības vai valsts sektorā. Apmeklējot kādu vietni, kur iespējams meklēt darbu, varat uzzināt, kādas darba vietas ir pieejamas matemātikas entuziastiem.
Cerams, ka līdz šim esat pārliecinājušies, ka matemātikas nodarbības liek jūsu neironiem aktivizēties un var jūs aizvest daudzviet! Un pavisam noteikti, ja zināt, kur meklēt, ir viegli pamanīt matemātikas nospiedumus mūsu ikdienas dzīvē!
Rezumēt ar MI















